IntroduzioneUn tempo, l’arte di programmare giochi bidimensionali era scienza di pochi. Non tutti, infatti, erano capaci di scrivere algoritmi ultra-ottimizzati in Assembler per la gestione delle “bitmap” a schermo. Per fortuna oggigiorno, grazie ad aziende come Nvidia, ATI, Matrox e la defunta 3DFX Interactive e molte altre, abbiamo nelle nostre case delle macchine potentissime e facilissime da programmare. Fare 2D al giorno d’oggi è abbastanza differente da come si faceva qualche anno fa.
Una piccola nota per chi ha utilizzato precedenti versioni di DirectX: DirectDraw, il componente di DirectX dedicato alla grafica 2D non esiste più in DirectXGraphics. Questo perché il consentire l’accesso al framebuffer (cioè direttamente ai pixel che rappresentano il video) era un forte fattore limitante per chi scriveva i driver. La maggior parte degli algoritmi di Anti-Aliasing a tutto schermo per esempio (una tecnica che serve per “smussare” le scalettature dei poligoni e non solo) lavorano attraverso il super-sampling. Questa tecnica consiste nel renderizzare la scena in uno schermo “virtuale” molto più grande della risoluzione fisica dello schermo e poi ridimensionare quest’immagine filtrandola per mandarla a video. Consentire l’accesso al “Front Buffer” sarebbe stato troppo complicato ed inefficiente da gestire quindi si è preferito negare agli sviluppatori tale possibilità.
Non crediate però che in DirectX8 non si possa più fare grafica 2D!!!Anzi, come potrete vedere nella lettura di questo capitolo, le possibilità sono aumentate dato che abbiamo a disposizione “gratis” una serie di effetti come per esempio alpha blending, rotazioni e tante altre cose.
Geometrie 2DLa matematica alla base della programmazione grafica 2D (se non si vogliono fare cose troppo complicate) è veramente poca, i primi anni di un qualsiasi istituto superiore saranno più che sufficienti.
In Computer Grafica (da ora in poi CG), non si può parlare di punti e di linee se prima non si fissa un’unità di misura ed un sistema di riferimento. L’unità di misura naturale della CG è il “pixel” che, come sicuramente già sapete, significa “picture element” e sta ad indicare uno dei tantissimi “puntini” che compongono l’immagine emessa dal vostro monitor. Il numero di pixel presenti in una scena dipende dalle dimensioni dell’area di disegno (rendering) dove si effettuano tutte le operazioni di disegno. Come visto nei precedenti articoli possiamo selezionare, grazie al nostro framework, una serie di risoluzioni per infittire questa “maglia di pixel” a schermo, in modo da ottenere una maggiore definizione dell’immagine.
Il sistema di riferimento per eccellenza è ovviamente quello cartesiano. L’unica cosa alla quale bisogna stare attenti è che l’origine degli assi è nell’angolo in alto a sinistra dell’area di rendering: l’asse delle Y ha il verso dall’alto in basso e l’asse delle X va da sinistra verso destra.
Disegnare quindi una linea dal punto di coordinate (0,0) al punto (10, 10) significa partire dall’angolo in alto a sinistra della finestra di rendering ed andare 10 pixel a destra e dieci pixel verso il basso. Detto questo userò sempre il sistema cartesiano con l’asse Y rivolto verso l’alto, per questioni di chiarezza. Se doveste implementare qualsiasi formula basterebbe invertire di segno la Y ed e’ fatta.
Un segmento in CG è rappresentato da un insieme di pixel opportunamente allineati. I poligoni (2D) sono formati da un insieme di segmenti. Non esistono linee curve in CG, o meglio, quelle che definiamo “curve” non sono altro che una serie di spezzate, formate da tanti piccoli segmenti, che ci danno “l’illusione” di rappresentare una curva. Più piccoli sono i segmenti che approssimano la curva minore è l’errore che commettiamo in quest’approssimazione.
Attraverso questa primitiva, il “pixel”, possiamo costruire tutto quello che ci viene in mente.
Consideriamo ora un’entità bidimensionale “rigida” qualsiasi, dove per “rigida” si intende che la distanza tra due suoi punti qualunque rimane costante. “Rigido” è esattamente il significato pratico che diamo alla parola, se capiamo la differenza tra una pietra ed un tovagliolo. Per semplicità immaginate quest’entità come un semplice quadrato o un rettangolo. Quali sono i movimenti elementari indipendenti che questo quadrato può effettuare? Tali movimenti sono esattamente tre: traslazione sull’asse X, traslazione sull’asse Y e rotazione attorno ad un punto, che scegliamo arbitrariamente coincidente con il centro del sistema di riferimento. Questo vuol dire che la configurazione del corpo è identificata univocamente da tre parametri (detti anche parametri normali in Meccanica Razionale per esempio) e, com’è naturale che sia, essi saranno la posizione del quadrato e un angolo di rotazione. Attraverso le più strane combinazioni di questi parametri potrete far muovere il quadrato ovunque nello spazio 2D, in tutti i suoi “gradi di libertà”. Il grado di libertà di un oggetto è sostanzialmente il numero di parametri indipendenti che ne individuano univocamente una configurazione nello spazio. Nel nostro caso i gradi di libertà sono tre (traslazione x, y e rotazione).
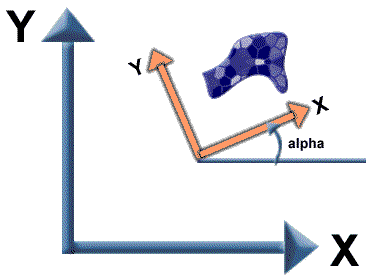
Detto in altri termini questi tre parametri ci permettono di “Trasformare” ogni singolo punto del sistema e portarlo in un nuovo sistema di riferimento. In termini matematici:
Per la rotazione (attorno all’origine del sistema di riferimento) di un angolo Alpha:
Per la traslazione
Se questo corpo ruota e si muove contemporaneamente allora basterà combinare linearmente queste equazioni:
Sarebbe comodo esprimere questa trasformazione con una matrice, ma se prendessimo quest’equazione così com’è ci troveremmo in difficoltà, poiché essendo una matrice 3 x 2 non possiamo sfruttare (facilmente) molte proprietà delle matrici quadrate. Utilizziamo allora un “trucco”, facciamo finta che il nostro punto sia “tridimensionale” e utilizziamo una matrice 3 x 3, ignorando la trasformazione dell’ultima coordinata che non ci interessa ponendola a 1:
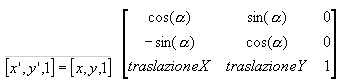
Una regoletta pratica per ricordare questa matrice di uso frequente è il seguente: mettete coseno e seno nella prima riga (come fareste normalmente associando la x al coseno e la y al seno) e nella seconda le rispettive derivate. Il bello di questa rappresentazione della trasformazione è che possiamo sfruttare tutte le proprietà delle matrici. Per esempio possiamo applicare più trasformazioni successive ad una stessa entità, sfruttando la moltiplicazione righe per colonne delle matrici, oppure possiamo “invertire” una trasformazione, invertendo appunto la matrice. A dire la verità semplici considerazioni geometriche ci fanno notare che la matrice inversa di quella che abbiamo scritto è semplicemente:
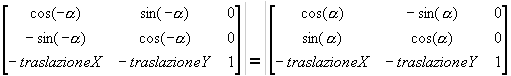
Quello che abbiamo fatto è stato semplicemente trasformare usando l’opposto della traslazione e dell’angolo nella matrice di prima. Come vedete sviluppando cambiano i segni dei due seni e della traslazione. Potete anche considerare il minore del secondo ordine in alto a sinistra come una matrice ortogonale e per invertirla basta prendere la trasposta. Il trucco però non si ferma qui!!!
DirectX è un’API incentrata sul 3D, dove facendo un ragionamento assolutamente analogo a questo si utilizzano matrici 4 x 4 per esprimere la configurazione di un punto in tre dimensioni. Per questo motivo anche quando rappresentiamo trasformazioni bidimensionali in DirectX dobbiamo usare una matrice del genere:
Come vedremo più avanti questa è la tipologia di matrice che si aspetta il metodo ID3DXSprite::DrawTransform().
Per creare questa matrice non serve andare ad aprire un libro di algebra linare, ma possiamo tranquillamente usare le funzioni della comodissima libreria D3DX di Microsoft in questo modo:
D3DXMATRIX result;
float alpha = D3DX_PI/2;
D3DXMatrixRotationZ(&result,alpha);
result._31 = traslazioneX;
result._32 = traslazioneY;
Come vedete sfruttiamo la funzione di rotazione attorno all’asse Z, il quale essendo perpendicolare a X e Y, ci fa ruotare sul piano XY che è proprio quello dello schermo.
Oltre a questo dobbiamo impostare “manualmente” gli elementi della matrice che rappresentano la traslazione dell’oggetto. Come vedete DirectX usa il formato [RIGA][COLONNA] per indicizzare gli elementi della matrice. Un altro vantaggio dell’utilizzo delle matrici è la possibilità di combinare le trasformazioni come già detto:
D3DXMATRIX t1, t2,result;
//eseguiamo delle operazioni su t1 e t2...
D3DXMatrixMultiply(&result,&t1,&t2);
//result ora contiene il risultato delle
//singole trasformazioni t1 e t2!
Per combinare le matrici potete usare anche il simbolo di moltiplicazione “*” giacchè D3DX effettua l’overloading degli operatori per le classi matematiche fondamentali.
D3DXMATRIX t1, t2,result;
result = t1*t2;
Questo codice fa lo stesso del precedente.
Render StatePrima di iniziare qualunque digressione su DirectX bisogna introdurre e capire il concetto di “Render State”. Se immaginiamo che la nostra scheda video sia un semplice televisore, potremmo definire i Render State come dei “pulsanti” o delle “manopole” che ci permettono di attivare/disattivare/modificare diverse opzioni di disegno.
Ci sono render state per qualunque cosa, per abilitare il filtering, lo zbuffer, lo stenciling etc. Ovviamente il significato dei singoli render state e la loro combinazione è specifico dell’effetto che si intende ottenere, ma per ora ci basta sapere che i render state si impostano nella forma:
lpDev->SetRenderState(RENDERSTATE, VALORE);
Vertex BufferBene, abbiamo capito che per mettere qualcosa a video bisogna sostanzialmente disegnare dei punti. Attraverso le matrici possiamo spostarli dove ci pare ma manca un dettaglio fondamentale…Come facciamo a disegnarli?
E’ proprio ora che entrano in gioco i Vertex e Index Buffer.
Potete immaginare un Vertex Buffer (da ora VB) come un vettore di vertici, dove ogni elemento indica a DirectX la posizione del punto da disegnare sullo schermo. In realtà ogni elemento di un vertex buffer può contenere oltre la posizione del vertice altre informazioni da passare a Direct3D, quali ad esempio il colore o le coordinate texture (come vedremo fra poco).
Un vertex buffer in Direct3D è rappresentato dall’oggetto COM IDirect3DVertexBuffer8 creabile attraverso IDirect3DDevice::CreateVertexBuffer(…)
struct CUSTOMVERTEX
{
D3DXVECTOR3 position; // vertex position
DWORD color; // vertex color
};
#define D3DFVF_CUSTOMVERTEX (D3DFVF_XYZ|D3DFVF_COLOR) m_pd3dDevice->CreateVertexBuffer(
numVertices*sizeof(CUSTOMVERTEX),
0, D3DFVF_CUSTOMVERTEX,
D3DPOOL_MANAGED, &m_pVB)
Come potete ben vedere i passi necessari per creare un vertex buffer sono semplici: si crea una classe o struttura che rappresenta il singolo vertice del vertex buffer (in questo caso abbiamo la posizione ed il colore del vertice), si definisce il cosiddetto FVF (Flexible Vertex Format) e si chiede al device di creare un VB della dimensione specificata (in bytes) con quel FVF.
Il FVF è una variabile DWORD contenente dei flag combinati tra loro tramite un OR binario. Questi flag servono per dire a Direct3D il TIPO delle informazioni contenute nella struttura. Sbagliare a combinare questi flag porterebbe ad una serie d’errori durante il rendering. Ecco alcuni esempi di strutture con relativi FVF:
//Questo vertice contiene solo posizione e spazio per 1 set di coordinate texture.
class DX8Vertex
{
public:
D3DXVECTOR3 posizione;
float u, v;
};
const DWORD DX8Vertex_FVF = D3DFVF_XYZ|D3DFVF_TEX1;
//Questo vertice ha spazio per la posizione e due set di coordinate texture (per multitexturing come vedremo avanti)
//Un vertice con posizione
class DX8Vertex
{
public:
D3DXVECTOR3 posizione;
float u, v;
float lu,lv;
};
const DWORD DX8Vertex_FVF = D3DFVF_XYZ|D3DFVF_TEX2;
//Questo vertice ha spazio per posizione, normale del vertice e due set di coordinate texture
class DX8Vertex
{
public:
D3DXVECTOR3 posizione;
D3DXVECTOR3 normale;
float u, v;
float lu,lv;
};
const DWORD DX8Vertex_FVF = D3DFVF_XYZ|D3DFVF_NORMAL|D3DFVF_TEX2;
Quando utilizzate questo metodo per comunicare a D3D il tipo dei campi del vostro vertice “personalizzato”, state attenti all’ordine nel quale li definite che in generale è:
- POSIZIONE
- PESI DI BLENDING
- NORMALE
- DIMENSIONE PUNTO (per point sprites)
- COLORE DIFFUSO
- COLORE SPECULARE
- COORDINATE TEXTURE 1
- …
- COORDINATE TEXTURE 8
Non vi preoccupate se alcuni di questi attributi vi sono sconosciuti, essi saranno trattati nei prossimi articoli. Mi raccomando, tenete a mente questa scaletta quando create dei FVF per i vostri VB.
Se il vostro FVF contiene una posizione, D3D provvederà a trasformare il punto usando le matrici che gli sono state passate (vedremo come). Dopo una serie di trasformazioni il punto in considerazione sarà disegnato sullo schermo, quindi attraverso coordinate 2D in pixel come quelle descritte nel paragrafo “Geometrie 2D”. Ci sono dei casi però dove NON desideriamo che D3D effettui per noi queste trasformazioni, ma vogliamo semplicemente che usi i valori che gli passiamo. In questo caso oltre alla posizione bisogna aggiungere un valore float chiamato w (coordinata omogenea) che per ora non ci interessa e dobbiamo riempire sempre con il valore 1.
Ecco qui un esempio:
class DX8Vertex
{
public:
float x,y,z,w;
D3DXVECTOR3 normale;
float u, v;
float lu,lv;
};
const DWORD DX8Vertex_FVF = D3DFVF_XYZRHW|D3DFVF_NORMAL|D3DFVF_TEX2;
Quando usiamo questo tipo di FVF, x e y rappresentano le coordinate fisiche effettive del pixel a schermo (relative all’angolo in alto a sinistra del device di rendering, che di solito è lo stesso dell’area client della finestra sulla quale disegnamo). Insomma per farla breve ci basterà inserire in x e y le coordinate che ci piacciono e D3D le userà così come sono. So che potrebbe sembrare tutto un po’ complicato, nel senso che ci si potrebbe chiedere a che servono quelle variabili (z e w) se non sono usate. La risposta sta nel fatto che stiamo facendo 2D “Accelerato”, quindi stiamo “aggirando” una serie di problematiche che affronteremo nel 3D vero e proprio. Non spaventatevi, come vedrete quando parleremo di sprite ci sarà una comodissima classe di D3DX che fa tutto il lavoraccio per noi. Mi raccomando, il flag da passare è D3DFVF_XYZRHW, se passate soloD3DFVF_XYZ in questo caso non funzionerà nulla.
Tornando ai Vertex Buffer, ecco qui l’esempio QuadratoArcobaleno (abituatevi ai nomi strani degli esempi):
struct MyVertex
{
D3DXVECTOR2 pos;
float z,w;
DWORD color;
};
const DWORD MyVertex_FVF = (D3DFVF_XYZRHW|D3DFVF_DIFFUSE);
class QuadratoArcobaleno : public DXGObject
{
IDirect3DVertexBuffer8* vb;
public:
QuadratoArcobaleno()
{
vb = 0;
}
bool OnCreateDeviceObjects()
{
HRESULT hr;
hr = GetDevice()->CreateVertexBuffer(
4*sizeof(MyVertex),
D3DUSAGE_WRITEONLY,
MyVertex_FVF,
D3DPOOL_MANAGED,
&vb);
CHECKHR(hr);
return true;
}
bool OnReleaseDeviceObjects()
{
SURERELEASE(vb);
return true;
}
bool OnRestoreDeviceObjects()
{
GetDevice()->SetRenderState(D3DRS_DITHERENABLE,TRUE);
GetDevice()->SetRenderState(D3DRS_ZWRITEENABLE,FALSE);
GetDevice()->SetRenderState(D3DRS_ZENABLE, FALSE);
return true;
}
bool OnDraw()
{
HRESULT hr;
IDirect3DDevice8* lpDev = GetDevice();
D3DVIEWPORT8 view;
GetDevice()->GetViewport(&view);
MyVertex* vertices;
hr = vb->Lock(0,0,(BYTE**)&vertices,D3DLOCK_NOSYSLOCK);
CHECKHR(hr);
float t = wrapper->fTime;
//Animiamo un pò i colori...
vertices[0].color = D3DCOLOR_XRGB((BYTE)(128*fabs(2*sinf(t*2))),0,0);
vertices[1].color = D3DCOLOR_XRGB(0,(BYTE)(255*fabs(sinf(t))),0);
vertices[2].color = D3DCOLOR_XRGB(0,0,(BYTE)(255*fabs(sinf(t*3))));
vertices[3].color = D3DCOLOR_XRGB((BYTE)(255*fabs(sinf(t*4))),255,0);
vertices[0].pos = D3DXVECTOR2(0,0);
vertices[1].pos = D3DXVECTOR2(view.Width ,0);
vertices[2].pos = D3DXVECTOR2(view.Width,view.Height);
vertices[3].pos = D3DXVECTOR2(0,view.Height);
vertices[0].z = vertices[0].w = 1.0f;
vertices[1].z = vertices[1].w = 1.0f;
vertices[2].z = vertices[2].w = 1.0f;
vertices[3].z = vertices[3].w = 1.0f;
vb->Unlock();
GetDevice()->SetVertexShader(MyVertex_FVF);
GetDevice()->SetStreamSource(0,vb,sizeof(MyVertex));
GetDevice()->DrawPrimitive(D3DPT_TRIANGLEFAN,0,2);
return true;
}
};
Come potete vedere abbiamo dichiarato la struttura vertice e il relativo FVF, poi abbiamo creato il vertex buffer. Voglio far notare che abbiamo creato il VB nel pool D3DPOOL_MANAGED quindi sarà Direct3D ad occuparsi di lui in caso di eventi “lost device”, ed è per questo che esso è creato in OnCreateDeviceObject() (chiamato solo alla creazione del device) e non in OnRestoreDeviceObject() (chiamato dopo ogni evento “lost device”). In OnDraw() c’e’ il grosso del programma, ma come potete vedere non è nulla di particolare: attraverso IDirect3DVertexBuffer::Lock() accediamo ai contenuti del VB e lo trattiamo esattamente come se fosse un array. Questo array è grande esattamente 4*sizeof(MyVertex), come indicato nella fase di creazione del VB. Volendo potremmo effettuare il locking anche solo di una parte dell’intero VB, tecnica che useremo per i VB dinamici. Scriviamo quattro vertici con coordinate ai quattro estremi del device di rendering (usiamo GetViewPort() per prenderne le dimensioni), e impostiamo dei colori “a caso” per ogni vertice. I parametri z e w, necessari per il 3D come già detto, non c’interessano e li poniamo uguali ad uno.
Dopo aver terminato la fase di scrittura nel VB (ricordatevi di chiamare Unlock altrimenti il programma fallirà), l’ultimo passo è settare il FVF con IDirect3DDevice8::SetVertexShader, impostare il VB dal quale effettuare il rendering con IDirect3DDevice8::SetStreamSource, passando il VB e la dimensione del singolo vertice ed infine disegniamo i 2 triangoli che compongono il “quadrato arcobaleno” con IDirect3DDevice8::DrawPrimitive(…). L’utilizzo di DrawPrimitive sarà spiegato in dettaglio nel capitolo sul 3D, per ora ci basta sapere che chiamando questa funzione con quei parametri vengono disegnati due triangoli rettangoli disposti a formare un quadrato. Ricapitolando:
- AVVIO PROGRAMMA: creazione del VB con IDirect3DDevice::CreateVertexBuffer
- “QUANDO SERVE” (cioè solo all’avvio se i dati sono statici oppure ad ogni frame se sono dinamici) si effettua il Lock, si scrive nell’array ritornato, si effettua l’Unlock. Se si riceve un “lost device” e il vertex buffer è dichiarato come D3DPOOL_MANAGED non dovrete preoccuparvi di nulla,ci pensa Direct3D.
- AD OGNI FRAME: per disegnare
- IDirect3DDevice8::SetVertexShader(MyVertex_FVF)
- IDirect3DDevice8::SetStreamSource(0,vb,sizeof(MyVertex))
- IDirect3DDevice8::DrawPrimitive con i parametri appropriati (ancora da descrivere)
La filosofia del Lock()/Unlock è fondamentale nella gestione delle risorse in Direct3D. Quando dobbiamo accedere direttamente ai dati di una qualsiasi risorsa, dobbiamo farlo attraverso Lock(). Non sempre è possibile fare quest’operazione, ad esempio le texture create con D3DPOOL_DEFAULT non possono essere “lockate”. L’operazione di Lock() è, in generale, dispendiosa per l’acceleratore perché deve prendere i dati dalla sua memoria, mandarli attraverso il BUS, farli usare al programmatore e farli ripassare per il BUS per aggiornare la sua copia in memoria video. Proprio per questo bisogna sempre specificare quando si creano risorse e si effettuano Lock() dei flag, che indicheranno a D3D cosa si intende fare.
Come vedete ho passato D3DUSAGE_WRITEONLY nella procedura di creazione del VB. Facendo questo ho praticamente detto al driver della scheda video che non c’e’ bisogno che il contenuto del VB sia esattamente quello riempito dal frame precedente. A me interessa solamente scrivere il quel VB, quindi non c’e’ bisogno che mi mandi indietro attraverso il BUS i dati originali presenti in memoria video. Quello che sto facendo è impostare una sorta di “senso unico” nella comunicazione dei dati al VB. Ovviamente questo significa che se provo a leggere dal VB otterrò semplicemente dei valori a casaccio, senza alcun significato. Esiste anche un flag D3DUSAGE_READONLY che si comporta analogamente nel caso opposto. Se non è specificato uno di questi due flags, la comunicazione è bidirezionale, si hanno permessi di lettura/scrittura sul VB.
Nel nostro esempio stiamo effettuando il lock del VB ad ogni frame ma questo non è assolutamente un buon metodo da usare. In generale la geometria STATICA è più facile da gestire di quella DINAMICA per un acceleratore video. In quest’ultimo caso bisogna utilizzare dei flag particolari e dei “pattern” di utilizzo dei VB, di cui potete trovare i dettagli sui papers della
http://www.nvidia.com ">Nvidia .